Mise à jour Mars 2013

I) Arithmomètre de 1848 (T1849)


L'arithmomètre T1848 possède un mécanisme de retenue tout à fait étonnant ! Celui-ci a été considérablement simplifié. La roue de retenue, présente sur T1820 et T1822, a été abandonnée. Tout le système qui permettait son déplacement l'a été également ! (Fourchette /double bras, axe rond, ressort à boudin). En lieu et place de tout cela, une dent de retenue extractible logée dans le corps du cylindre a été mise au point. Un ressort, monté sur le même axe tend naturellement à la faire sortir. Ceci est rendu possible par le biais d'une pièce cylindrique X qui est raccordée à la dent par un petit bras perpendiculaire. La dent possède deux fentes inclinées qui coulissent sur des goupilles. Sous l'effet du ressort, la dent glisse sur elles, ce qui la fait sortir du cylindre. En phase neutre, l'action combinée d'un colimaçon et d'un cliquet empêche la dent de sortir. Notons au passage que ce système de blocage est quasi identique à T1822...Bref.. Au passage de 9 à 0 d'un des cadrans du totalisateur, une petite cheville, placée sous le cadran provoque l'échappement d'un cliquet. Parallèlement, le colimacon perd sa fonction de blocage pendant la rotation du cylindre. Plus rien ne s'oppose alors à la détente du ressort et à la sortie de la dent extractible. Pour pouvoir effectuer la retenue, la dent de retenue a été allongée de telle manière que celle-ci puisse engrener avec la roue coulissante A, quelque soit sa position le long du cylindre (de 0 à 9). En fin de rotation, une rampe hélicoïdale recomprime le ressort et fait rentrer la dent dans le cylindre, le colimaçon et le cliquet bloquant à nouveau l'ensemble.

Le dent extractible de T1848

Phase neutre

Phase de retenue

Platine supérieure de T1848

II) Sources

"Brevet N° 8282 du 25 avril 1849"

Extrait :

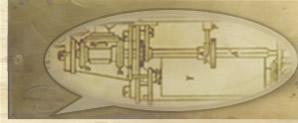
« Au dessous de chaque cadran est fixé une roue à 10 dents et le cadran porte une pointe ou un petit bras qui fait partir une détente lorsque le cadran passe du 9 au 0 ou du 0 au 9 (Voir fig.1 & fig.2)

 Dans l’intérieur, on voit (figure 2) des cylindres cannelés de 20 dents dont on en a coupé onze sur toute la longueur, puis les neuf restantes sont coupées par neuvièmes, en forme d’escalier pour représenter le chiffre du multiplicande de 1 à 9  (voir la figure 5 qui représente un des cylindres, ils ont 0m07 de longueur).
Une dixième dent mobile est placée à la suite des 9 dents comme il est expliqué ci-après.

 Les dents des cylindres peuvent engrener dans une petite roue de dix dents qui est conduite par une fourche attachée au bouton indicateur. La petite roue glisse sur un arbre carré et se laisse conduire au chiffre du multiplicande. Alors cette place la fait engrener à la section des dents dont le nombre est égal au chiffre indiqué par le bouton.
Quand le cylindre a fait un tour, il a tourné la petite roue du nombre de dents qu’indique le chiffre et le cadran a rendu ce chiffre visible.
Un cliquet soulevé par les dents des cylindres accompagne les petites roues. Lorsqu’elles ne sont plus en prise avec les dents du cylindre, le cliquet tombe et les arrête. 

A la gauche de ces cylindres est un autre cylindre taillé en spirale (voir figure 7). Une fente taillée dans sa longueur permet à un bras conduit par un bouton, de régler le nombre de tours que les cylindres doivent faire ensemble pour représenter un des chiffres du multiplicateur.

Ainsi quand le bouton du multiplicateur est au N° 9, le multiplicande, fut-il de dix chiffres, sera multiplié par 9.

Tous les cylindres du multiplicande, y compris celui du multiplicateur engrènent dans une suite de roues, dont l’une sera armée d’une manivelle, de manière que chaque tour de manivelle fait faire un tour à tous les cylindres ensemble (voir cet engrenage figure 3).

On obtient ce même mouvement par un arbre placé sur la longueur de la platine engrenant  [….] roues de champ, avec celles des cylindres. Ce mouvement est bien meilleur, mais il est plus dispendieux. 

Sur les cylindres placés entre le premier et le dernier, il y a un système d’engrenage pour opérer les retenues. Une dent mobile, qui prend toute la longueur du cylindre, remplace la dixième dent. Elle est cachée dans l’épaisseur du cylindre (Fig. 6) et ne parait au niveau des autres dents pour engrener avec la petite roue que pour produire la retenue (Fig. 6)

Pour produire cet effet, un ressort à boudin sur l’arbre du cylindre, comme on le voit figure 6, pousse  la dent à sortir sur deux plans inclinés ; Un plan incliné fixé sur la platine comprime le ressort en repoussant la dent à chaque tour de cylindre ; Un petit bras qui communique avec le cadran de droite tient le ressort bandé pendant tout le temps qu’il n’y a pas de retenue à reporter, mais lorsque le cadran passe du 9 au 0 ou du 0 au 9, la petite cheville ou le petit bras du cadran fait partir le cliquet, et le ressort pousse la dent du chiffre de gauche, et quand le chiffre est produit, la retenue vient s’ajouter.

 C’est ici le cas d’expliquer pourquoi on a coupé entièrement onze dents des cylindres ; Ce vide était indispensable pour opérer les retenues ; Il faut que chaque cylindre puisse recevoir la retenue après avoir produit son chiffre. Pour que cela puisse avoir lieu, il faut que les retenues se fassent successivement l’une après l’autre : il a donc fallu que les dizaines se produisent avant les centaines, celles des centaines avant celle des milles et ainsi de suite. C’est pourquoi il faut placer les cylindres de manière à engrener avec les roues du chiffre multiplicande les uns après les autres. On doit laisser 2 dents de différence entre chaque cylindre ; C’est-à-dire le second cylindre aura 2 dents de vide, le troisième 4 dents, le cinquième 6 dents, le sixième 8 dents.
Chaque cylindre doit avoir deux dents de coupées par chaque chiffre du multiplicande, pour lequel la machine est construite, plus une pour la retenue, ce qui fait pour la machine à cinq chiffres onze dents.»

www.arithmometre.org
2013