Mise à jour Mars 2013

I) Arithmomètre de 1822 (T1822)

Le modèle T1822 est exceptionnel ! C'est à ce jour le plus ancien arithmomètre connu. On ignore si Thomas en avait construit plusieurs exemplaires. Ce petit bijou est aujourd'hui conservé au Smithonian Institute (NMAH) de Washington. Sur le plan technique, la machine est très différente de celle décrite dans le brevet N° 1420 de 1820. C'est un modèle de "deuxième génération" dont le Bulletin de la Société d'encouragement pour l'industrie nationale de 1822 fournit les caractéristiques détaillées.

Smithsonian Institution, Washington

a) Mécanisme de retenue

La "10e dent" du cylindre de T1820 a migré et s'est transformée en une pièce Z, positionnée après le cylindre, dans son prolongement. Sa fonction est, lors de la phase de retenue, d'engrener avec la roue f de la décade N+1 . Une roue conique J, montée sur le même axe, transmet alors une unité à la roue totalisatrice K. Sur T1822, une unité correspond à l'avancement de deux dents (voir chapitre sur les cylindres).

Détail du mécanisme de T1822 / Vue latérale

Le processus de retenue se décompose comme suit: La roue f est reliée à un double bras xy qui provoque son déplacement. En position de "repos", un pièce a en forme de colimaçon garde xy tendu. Dans cette configuration, la roue f est légèrement décentrée par rapport à la dent z et ne peut engrener avec elle. Une goupille, retenue par un cliquet, maintient également ce statut quo. Au passage de 9 à 0 d'un des cadrans du totalisateur, une double libération se produit. D'une part, un petit plan incliné placé sous le cadran provoque l'échappement du cliquet. Parallèlement à cela, la rotation des cylindres fait tourner le colimaçon et libère pendant un temps donné xy de sa tension. Les deux forces qui maintenaient la roue f en position neutre (tendue) sont momentanément désactivées. Celle-ci avance alors de quelques millimètres et vient se placer dans le giron de la dent z. La retenue peut s’effectuer ! En fin de rotation, "a" va  re-comprimer le ressort et le garder tendu. Le cliquet retrouve égallement sa place et empêche la goupille d'avancer. Le tour est joué ....Ouf ...

Détail du mécanisme de T1822 / Vue supérieure

Détail du mécanisme de T1822 / Vue arrière

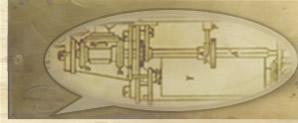
Si vous souhaitez plus de détails sur le fonctionnement de ce superbe arithmomètre, je vous invite à lire le Bulletin de la Société d'encouragement pour l'Industrie Nationale de Novembre 1822. Celui-ci y est décrit de manière remarquable par Hoyau. Je vous ai rajouté les liens vers les illustrations dans le corps même du texte. Bonne lecture !

« C’est en cherchant à remplacer l’adresse ou l’intelligence par des procédés mécaniques que l’on est parvenu à perfectionner les arts utiles, à augmenter la quantité des produits, à en diminuer le prix, et à répandre sur toutes les classes de la société les bienfaits de l’industrie ; mais si quelques opérations manuelles ont été suppléées avec succès par des mécanismes ingénieux, il semble bien difficile de substituer à des raisonnements fondés sur des théorèmes scientifiques des moyens purement mécaniques, et d’en obtenir les conséquences.

Cependant, de toutes les sciences crées par l’intelligence humaine, les mathématiques sont celles qui offraient le plus de chances de succès, puisque c’est du calcul que l’on déduit les combinaisons mécaniques, et que, par un juste retour, ces combinaisons devaient offrir les résultats du calcul : aussi les philosophes de tous les âges se sont-ils exercés à rendre plus facile l’application des mathématiques aux usages de la vie,  soit en simplifiant les raisonnements de la science, soit en les remplaçant par des opérations manuelles qui soulageaient l’intelligence ou tout au moins la mémoire. Ainsi les Orientaux calculaient avec des grains enfilés sur des broches parallèles ; les Romains employaient des jetons ; enfin, pour plus de facilité, on a fait usage des doigts, et toutes ces méthodes apportaient plus ou moins de facilité dans les opérations ; mais de tous les modes abréviateurs, le plus puissant et le plus fécond est, sans contredit, celui qui est dû à l’invention des logarithmes.

Par leur usage, on ramène les opérations d’un ordre supérieur à celles dont les résultats sont les plus faciles à trouver ; et des calculs pénibles, longs et sujets à des erreurs fréquentes, par la fatigue qu’ils font éprouver, ont été remplacés par des raisonnements si simples, que les erreurs deviennent presque impossibles, si l’on y porte la plus légère attention ; enfin, la réduction des logarithmes en lignes a donné naissance à des instruments portatifs d’une simplicité admirable et d’un emploi tellement facile, que l’on doit justement s’étonner de ne pas avoir répandu avec plus de rapidité, en France, l’usage de la règle ou des cercles logarithmiques, tandis que dans toute l’Angleterre, il n’est  peut-être pas un seul constructeur auquel cet instrument ne soit familier.

Mais tous ces moyens exigent encore des connaissances scientifiques ou ne donnent que le résultat de certaines opérations : ainsi la règle logarithmique ne peut servir ni pour l’addition ni pour la soustraction.

Enfin Pascal essaya de remplacer par des moyens mécaniques les différentes opérations de l’arithmétique ; mais la machine qu’il composa était extrêmement compliquée, et laissait encore à désirer pour quelques opérations plus de simplicité ou plus de promptitude.

Si l’on pouvait assigner des bornes à nos facultés intellectuelles, il semblerait que tant de moyens découverts pour arriver à calculer mécaniquement ont épuisé les recherches en ce genre, et qu’il ne reste plus rien à faire après les savants célèbres de tous les pays, qui se sont occupés de cet objet.

Cependant M. le chevalier Thomas, de Colmar, est parvenu à vaincre toutes les difficultés, et à composer une machine qu’il a présentée à la Société d’Encouragement au mois de février dernier, et au moyen de laquelle on peut faire les quatre opérations de l’arithmétique : c’est de cette ingénieuse découverte que nous allons nous occuper.

Avant d’entrer dans le détail du mécanisme, nous rappellerons quelques principes mathématiques sur lesquels sa construction est fondée :

1° La multiplication est une addition abrégée d’une quantité avec elle-même

2° La division est une soustraction abrégée qui a pour objet de faire connaître combien de fois une quantité est contenue dans une autre. »

« L’arithmomètre ou machine à calculer de M. Thomas, se compose de deux platines A, B (fig. 1), tenues à distance par quatre piliers C, et recevant les pivots d’un certain nombre de roues et de tambours ou cylindres, qui forment le mécanisme.

Le premier cylindre D porte neuf encoches disposées en hélice autour de sa circonférence, et s’élevant par étage suivant sa longueur ; elles présentent à peu près l’aspect d’un escalier à marches très courtes, tournant autour d’une colonne. L’une des extrémités de ce cylindre porte un barillet E contenant un grand ressort qui tend constamment à le faire tourner dans le sens marqué par  la flèche. Le second cylindre F roule librement sur son axe ; il porte à l’un des ses bouts un pignon G, de vingt sept dents, qui fait corps avec lui, et à l’autre une roue à rochet H, que l’on voit en plan et détachée, fig. 9 : son axe I reçoit une roue K de cinquante-quatre dents. C’est cette dernière roue qui donne le mouvement au mécanisme ; elle porte une cheville r’, fig. 4, qui sert à arrêter sa marche. Le cylindre F communique son mouvement au cylindre D à l’aide du pignon G, qui engrène avec la roue L. Cette roue de quatre-vingt-une dents, n’est autre chose qu’une roue de renvoi, dont l’axe reçoit un pignon M, de vingt-sept dents, qui engrène avec la roue N,  de quatre-vingt-une dents, montée sur l’axe du premier cylindre D.

Au dessus du cylindre F est disposé un axe O, carré sur toute sa longueur : il porte à l’un de ses bouts un bras de levier fixe P, que nous nommerons « butoir d’arrêt » . Sur ce même axe coule une bague Q, dans laquelle on a pratiqué une gorge semblable à celle d’une poulie ; cette bague est munie d’un bras de levier R, dont l’extrémité s’avance jusqu’au fond des encoches du cylindre D. La gorge de la bague Q reçoit une fourchette T destinée à la transporter à différentes distances. Vers l’angle à gauche de la fig. 4, on aperçoit un petit butoir U contre lequel vient s’appuyer la cheville V , implantée sur la roue N. L’objet de ce butoir est de retenir le cylindre D et de borner l’action du ressort renfermé dans le barillet E.

Sans cet arrêt, le ressort se débanderait totalement, et les diverses pièces ne se replaceraient pas dans la position convenable. Le bec du butoir U est à charnière, afin de laisser passer la cheville V, lorsqu’on veut tendre le ressort en montant la machine.

Toute la partie du mécanisme que nous venons de décrire est en quelque sorte indépendante de celle qui sert au calcul ; elle lui donne le mouvement et règle le nombre de tours nécessaire au cylindre F, pour effectuer l’opération qu’on désire.

Le reste du mécanisme est composé de trois systèmes entièrement semblables entre eux, et pourrait l’être dans un plus grand nombre si on le désirait. Chacun de ces systèmes représente un rang de chiffres, en sorte qu’avec la machine figurée, fig.6, on ne peut obtenir que les résultats dans lesquels les facteurs n’ont que trois chiffres. Il nous suffira donc de décrire un de ces systèmes pour avoir fait connaître tous les autres.

La principale pièce est un cylindre X cannelé sur la moitié de sa circonférence, de manière à former dix-sept dents triangulaires. On le voit en plan et en élévation, fig. 7 et 8. La plus longue dent, qui est seule s’étend d’un bout à l’autre du cylindre ; les autres sont coupées deux à deux, à des longueurs qui forment un neuvième, deux neuvièmes, trois neuvièmes,  etc., de la longueur du cylindre. A l’extrémité de l’axe du cylindre est fixée une roue W de même nombre de dents que la roue K, et recevant son mouvement de celle-ci par l’intermédiaire de la roue Y, ayant aussi cinquante quatre dents. A L’autre extrémité du cylindre X sont deux petits bras de levier, dont l’un Z, se termine en pointe, et l’autre a, offre à son extrémité un petit plan incliné. A droite et au dessus du cylindre, on aperçoit un arbre carré b, portant trois roues dentées, dont deux sont mobiles : l’une c est percée d’un trou carré à travers lequel passe l’arbre ; elle fait corps avec une petite poulie d qui reçoit une fourchette e, fig. 4, servant à la transporter au point convenable du cylindre ; l’autre roue f, de même construction que la première, n’a qu’un très léger mouvement, par l’action des leviers Z et a fixés sur l’axe du cylindre X ; la troisième est une roue conique j, de vingt dents, fixée et immobile à l’extrémité de l’axe b.

Auprès de cet axe est placé un arbre rond g, dont le bout h traverse la platine supérieure : ce bout est retenue à fleur de la platine par un cliquet l’ qui s’oppose à l’effort du ressort à boudin i, lequel tend à faire sortir le bout de cet axe au dessus de la platine, jusqu’à ce qu’il s’appuie sur la portée k. L’arbre g est muni d’une fourchette l qui entre dans la gorge de la poulie de la roue f et d’un bras m, portant à son extrémité un plan incliné.

Les trois systèmes semblables à celui que nous venons de décrire communiquent entre eux au moyen de roues intermédiaires n, tournant sur des vis fixées à la platine inférieure.

La première roue intermédiaire Y, qui transmet du cylindre F au premier cylindre X, au lieu d’être montée, comme les roues n, sur une vis qui leur sert d’axe, est fixé sur un arbre p qui traverse la platine supérieure ; l’extrémité de cet arbre qui s’élève au dessus de la platine est munie d’une roue q, de quarante cinq dents, engrenant dans un pignon q’ de quinze dents, monté sur un volant en plomb r : ce volant est fixé sur un axe dont un des pivots roule dans un trou percé à travers la platine, et l’autre dans un trou pratiqué à l’extrémité d’un coq s : cette partie n’est pas absolument nécessaire, n’ayant d’autre objet que de régulariser l’effort à faire pour produire le mouvement.

Le mécanisme que l’on voit, (fig. 1),, est recouvert d’une platine t, fig. 6, à travers laquelle passent les queues des fourchettes c et celle de la fourchette T ; elles portent chacune un bouton u, à l’aide duquel on les fait glisser dans les entailles longitudinales v  : un petit index u  marque le chiffre auquel on veut faire correspondre la position de la fourchette. Le bouton à gauche, fig. 6, fait mouvoir la fourchette T, fig. 4, qui tient à la première partie de la machine. On aperçoit  auprès de l’entaille de ce bouton un autre petit bouton immobile x, qui est réuni à un petit bras de levier faisant corps avec le butoir d’arrêt P, fig. 4; il est comprimé par un ressort y qui écarte le butoir de la position où il fait arrêt. L’auteur nomme cette partie le régulateur, parce qu’il sert à fixer la première partie de la machine à la position convenable pour opérer.

Une troisième partie de la machine consiste dans un système de cadrans z, fig. 1 et 2. La platine sur laquelle ils sont montés est représentée par dessous, fig. 1.

Chaque cadran porte une roue d'angle a', de quarante dents, qui reçoit son mouvement de l'une des roues d'angle j ; sur ces roues a' sont fixés de petits plans inclinés b', dont nous indiquerons l'usage. Les ressorts c' que l'on aperçoit, fig. 1, sont destinés à établir contre la circonférence des cadrans un frottement qui les empêche de passer le point où ils doivent s'arrêter. Ces cadrans, dont l'un est dessiné séparément, fig. 10, sont divisés sur 2 cercles concentriques qui portent chacun les 10 chiffres sur chaque demi circonférence : ceux du cercle extérieur sont distingués des autres par une couleur différente.

Les premiers qui vont en croissant de gauche à droite se voient à travers les lunettes d', fig. 6; les seconds, qui sont disposés en sens contraire, sont aperçus à travers les ouvertures e' : une petite bande à coulisse, fixée sous la platine et qu'on fait mouvoir au moyen de l'onglet t', est percée de trous qui répondent à volonté aux lunettes d' ou e', de manière que quand les trous d' sont fermés, les autres sont ouverts et vice-versa. Les cadrans z portent à leur centre des boutons f', à l'aide desquels on peut les faire tourner avec les doigts ; enfin, la platine g' tourne autour d'une tringle h', fig. 1, portée par 3 supports i' : cette tringle passe dans des trous pratiqués aux extrémités des deux bras k qui tiennent à la platine A; ce qui forme une espèce de charnière autour de laquelle tout le système peut tourner, et même se transporter dans le sens de sa longueur.

La platine représentée, fig.2, est celle qui porte le volant et les cliquets d'arrêt des axes g : ces cliquets l' sont pressés contre les roues des cadrans par des ressorts m' ; les deux cliquets n' n' ne sont que deux ressorts qui servent à arrêter les cadrans à la position de zéro.

Le cylindre F est entouré d'un ruban de soie o' qui fait dix tours au moins sur ce cylindre : ce ruban passe à travers un petit tuyau p' fixé sur un des piliers d'écartement des platines ; par cette disposition il est dirigé sur le milieu du cylindre destiné à le recevoir. L'un de ses bouts est attaché à un point fixe sur le cylindre, l'autre porte un petit bouton s', à l'aide duquel on peut le tirer pour faire tourner le cylindre et donner le mouvement au mécanisme.

Telle est la machine inventée par M. le chevalier Thomas : elle parait fort compliquée, parce qu'il entre dans sa composition un assez grand nombre de pièces ; mais elle est réellement très simple : car les mêmes pièces y sont répétées plusieurs fois, ce qui était inévitable, comme nous allons le voir bientôt : l'inventeur se propose de la simplifier encore.

Il nous reste maintenant à faire connaître le jeu et les effets de la machine, et c'est par les détails dans lesquels nous allons entrer qu'on pourra juger des difficultés que M. Thomas a rencontrées, et des moyens ingénieux à l'aide desquels il a su les vaincre.

La machine, par sa disposition, imite parfaitement les opérations de l'arithmétique, et ses mouvements semblent peindre tous les raisonnements qu'il faut faire pour arriver au résultat.

Les cadrans peuvent devenir tout à fait indépendants du mécanisme, et pour cela il suffit de transporter les boutons u jusqu'au point où l'index w indique zéro : alors les roues c n'engrènent plus avec aucune partie des cylindres X, et ces cylindres se meuvent sans qu'il en résulte aucun changement. Si en même temps l'index du bouton u à gauche fig. 6, est au point marqué I, on pourra tirer le cordon, qui fera faire un tout au cylindre F, et amènera la cheville r', fig. 4, au point de buter contre la pièce P, que nous avons nommé "butoir d'arrêt". Le cylindre F ne pourra en effet développer qu'un tour ; car dans cette position le bras de levier R, qui tient à la boite coulante Q, sera pressé par la première encoche du cylindre D, et faisant culbuter la pièce P, arrêtera la roue K du cylindre F : alors le barillet E ramènera toutes les pièces, et la machine sera disposée pour le calcul.

Afin de faire comprendre plus facilement le jeu du mécanisme, nous allons indiquer les mouvements qu'il prend pour effectuer les quatre opérations de l'arithmétique.

Supposons que l’on veuille ajouter 4 à 2, tous les boutons u marquant zéro et la coulisse découvrant les ouvertures d’, on fera tourner le premier cadran à droite, jusqu’à ce qu’il montre par l’ouverture d’ le chiffre 2 ; on transportera ensuite l’index du premier bouton u à droite, jusqu’au trait marqué 4, alors la roue c à droite, fig. 1, se trouvera transporté au point du premier cylindre X, à droite, qui répond à la quatrième portion cannelé, c'est-à-dire au point ou ce cylindre, en tournant, fait passer huit dents de la roue c, celle-ci portant vingt dents ; si on tire le cordon o’, le cylindre fera un tour et elle fera quatre dixièmes de tour. La roue j engrène avec a’, qui est montée sur le premier cadran ; et comme cette dernière porte un nombre de dents double de la roue j, quarante dents, elle fera quatre dixièmes d’un demi-tour, ce qui aura fait passer quatre chiffres du cadran : il marquait 2, il indiquera donc quatre unités de plus, ou 6.

Si maintenant on voulait ajouter 7 à 6, le premier cadran marquant 6, on transportera le premier index u au point marqué 7, et il répondra à la partie du cylindre X, dont le nombre des cannelures fait faire sept divisions au cadran. Si on tire le cordon o’, le cylindre fera un tour, , et le cadran aura tourner de sept divisions et marquera 3 ; mais au moment ou le zéro a passé devant la lunette, le petit  plan incliné b’ du premier cadran a poussé le premier cliquet l’ ; alors le bout du premier petit arbre g, pressé par le ressort à boudin i, s’échappe, n’étant plus retenu par le cliquet, et la première roue f est soulevée de manière à se trouver dans le même plan que le petit bras Z du deuxième cylindre ; celui-ci faisant un tour, le bras Z rencontrera la roue f et la fera marcher de deux dents, c'est-à-dire d’une division du second cadran : ainsi ce cadran qui marquait zéro marquera 1 ; ce qui, avec 3 du premier cadran, donnera 13, somme de 7 et 6.

Ce dernier exemple, extrêmement simple, fait connaître le moyen employé pour marquer les retenues, ce que nous allons dire ne sera qu’une conséquence de ce qui précède.

Supposons que tous les cadrans marquent zéro, que l’index à gauche, que nous nommerons multiplicateur (ainsique l’indique le mot écrit prés de la coulisse), soit à 1, et que l’on écrive le nombre 237 sur les trois coulisses à droite, c'est-à-dire 7 sur la première, 3 sur la seconde, et 2 sur la troisième, ainsi que l’indiquent les mots unités, dizaines, centaines, écrits prés de chacune de ces coulisses : si l’on tire le cordon jusqu’à ce que l’on sente retenu par le butoir d’arrêt P, le nombre se trouvera écrit sur les trois premiers cadrans à gauche ; si maintenant on change  le nombre et qu’on écrive  394 sur les trois coulisses, en tirant le cordon, ce nombre sera ajouté à l’autre, et on lira à travers les lunettes d’ le produit, qui est 632. En effet, les unités en s’ajoutant auront fait faire une unité de plus que le demi tour du cadran ; le cliquet aura laissé échapper le petit arbre qui porte la fourchette l, la roue f sera élevée jusqu’au niveau du bras Z du second cylindre X, et celui-ci, dan,s son mouvement, lui aura fait faire une division de plus. Ce second cadran, considéré comme le premier, avait tourné en même temps et marqué neuf unités de plus que les trois dizaines qu’il offrait d’abord, en sorte qu’il a fait plus d’un demi tour, et par conséquent il a agi sur la roue du cylindre suivant, de manière à lui faire marquer une unité de retenue ; enfin le troisième cadran a marché de 3 unités, qui, avec 2 qu’il marquait déjà, ont fait 5, et de plus il a marché d’une division pour indiquer la retenue faite sur les deux chiffres précédents.

Si l’on fait attention à la manière dont les cylindres X sont cannelés, on verra que la moitié seulement de leur circonférence porte les cannelures, en sorte que les roues avec lesquelles ils engrènent restent en repos pendant toute une demi circonférence du mouvement ; c’est précisément pendant ce temps que les retenues se marquent, et avant que la seconde demi circonférence soit totalement achevée, le plan incliné a’, qui est monté sur le cylindre, a replacé le petit arbre g dans sa position ordinaire, c'est-à-dire qu’il a fait descendre son extrémité h au dessous du cliquet l’, qui, pressé par le ressort m’, a passé sur le bout de cet arbre g, et a replacé la ou les roues f, dans la position où les bras Z ne peuvent pas les rencontrer.

Maintenant la multiplication ne sera pas difficile à comprendre : en effet, si l’on suppose que l’on ait 25 à multiplier par 6, on placera les cadrans à zéro, on écrira 25, en plaçant l’index u aux chiffres 2 et 5 des dizaines et des unités sur les coulisses v ; on transportera l’index w du multiplicateur au chiffre 6 : alors si on tire le cordon, le cylindre F fera six tours, parce que le petit bras R répondra à la sixième encoche du cylindre D, en sorte que ce bras ne sera soulevé qu’après le sixième tour, et le butoir P ne s’opposera au mouvement de la roue K qu’à la fin de ce sixième tour. Or, nous venons de voir qu’un tour marquerait sur les cadrans le nombre qu’on avait écrit sur les coulisses, et qu’un nouveau tour ajouterait ce nombre à celui déjà marqué : ainsi, au second tour, on aura deux fois le nombre 25, au troisième, trois fois le nombre 25, et enfin au sixième, six fois ce nombre ou 150.

Soit à multiplier 643 par 237 ; on écrit 643 sur les trois coulisses, les cadrans marquant zéro : on place le multiplicateur à 7, on tire le cordon, et le premier produit partiel, 643 x 7 = 4501, est écrit sur les cadrans : alors on soulève la platine g’, et on désengrène les roues des cadrans d’avec celles j du mécanisme ; on fait glisser cette platine à droite jusqu’à ce qu’une petite pièce placée sous la platine tombe dans une encoche, qui l’arrête.

Par cette situation, le premier cadran droite cesse d’être en communication avec le mécanisme, et le second cadran engrène avec la roue des unités : alors toutes les dizaines fournies par le premier produit partiel restent écrites sur les cadrans. Si maintenant on remarque que le second produit partiel fourni par le chiffre des dizaines du multiplicateur ne peut donner que des dizaines, on verra que si l’on place l’index w du multiplicateur au chiffre 3, et qu’on tire le cordon, l’on obtiendra non seulement le second produit partiel de 643 x 3 = 1929, mais encore la somme de ce produit et des dizaines fournies par le produit obtenu de la multiplication par les unités, c'est-à-dire 23791.

Il est facile de voir que pour obtenir le produit par les centaines, il faut encore transporter la platine g’ des cadrans d’une division à droite : alors les deux premiers cadrans deviendront indépendants du mécanisme, et le cadran des centaines répondra aux unités du multiplicande ; mettant enfin l’index multiplicateur au chiffre 2, et tirant le cordon, le produit entier, 152391 sera écrit sur les cadrans.

Dans la machine que le dessin représente, on ne  peut employer qu’un multiplicateur de trois chiffres ; mais si on voulait avoir un produit plus élevé, on pourrait l’obtenir d’une machine qui serait formée d’un plus grand nombre de cadrans. M. Thomas se propose d’en construire, au moyen desquelles on amènera les produits de facteurs composé de cinq chiffres et même davantage.

Il nous reste à faire connaître la manière d’opérer la soustraction et la division : rien n’est plus simple que le moyen imaginé par l’auteur ; il consiste à diviser les cadrans sur un cercle concentrique en faisant croître les nombres en sens inverse des autres : par cette disposition,la marche du cadran, au lieu d’ajouter aux nombres qu’il présente autant d’unités qu’il a parcouru de divisions, retranche ce nombre d’unités, et le cadran marque cette différence.

Si l’on veut retrancher 4 de 6, on tirera d’abord la coulisse t’ et on découvrira les ouvertures e’ en même temps qu’on fermera celles d’ : alors la partie du cadran divisée en sens inverse se montrera à travers ces ouvertures. Tous les index w étant à zéro et le multiplicateur à 1, on fera paraître le chiffre 6 du premier cadran, on transportera l’index w à droite au chiffre 4, on tirera le cordon, et on verra paraître 2 sur ce premier cadran : cet effet semblera tout naturel, si l’on considère que la première roue mobile e’ a été transportée au point du cylindre X, qui fait faire quatre divisions au cadran, et que les divisions de ce cadran décroissent en sens inverse de la direction de son mouvement, d’où il résulte que ce cadran marquera 4 unités de moins.

Il sera facile de conclure par analogie que si les nombres de l’opération ont plusieurs chiffres, il suffira d’écrire le plus grand nombre sur les cadrans, et le plus petit  sur les coulisses w, et en tirant le cordon les centaines seront retranchées des centaines, les dizaines des dizaines, les unités des unités. Quant aux retenues de l’opération, elles se feront précisément comme pour l’addition ; mais le cadran, au lieu de marquer une dizaine ou une centaine de plus, offrira une dizaine ou une centaine de moins.

A l’égard de la division, elle se fera d’une manière inverse de la multiplication : soit à diviser 43627 par 329, on écrira le nombre 43627 sur les cadrans et le diviseur 329 sur les coulisses ; on transportera la première partie, 436, du dividende ou le premier dividende partiel au dessus de 329, en plaçant la platine des cadrans de manière que les deux premiers cadrans soient à droite en dehors de la machine : alors on aura disposé l’opération comme si l’on voulait retrancher 329 de 436. L’index multiplicateur marquant 1, on tirera le cordon, et on trouvera la différence 107 écrite sur les cadrans : si ce reste contenait encore le diviseur, on tirerait le cordon autant de fois qu’il serait nécessaire pour que le reste fût moindre que 329, et ce nombre de fois serait le nombre d’unités du premier chiffre à gauche du quotient. Le nombre restant sera donc 10727 : alors on transportera la platine g’ des cadrans à une division plus à gauche, et le chiffre 2 du dividende correspondra au chiffre 9 du diviseur. Si maintenant on laisse le multiplicateur à l’unité, il faudra tirer le cordon autant de fois que 329 est contenu dans 1072 ; mais au premier coup d’œil on voit facilement qu’il y en a trois : en conséquence, au lieu de tirer trois fois le cordon,on placera le multiplicateur au chiffre 3, et tirant le cordon,  le cylindre fera trois tours ; ce qui formera le produit 329 par 3, et en même temps le retranchera de 1072 : si le reste était encore plus grand que 329, on replacerait le multiplicateur à l’unité, on tirerait autant de fois qu’il serait nécessaire pour que le reste fût plus petit que 329, et l’on ajouterait à 3 autant d’unités qu’on a tiré de fois le cordon ; mais dans l’exemple que nous avons pris on trouve que le reste obtenu est plus petit que 329 : ainsi la première opération a suffi : on a donc les chiffres 1 et 3 du quotient ; enfin, plaçant le premier cadran vis-à-vis les unités du diviseur, et opérant comme précédemment, on obtiendra le chiffre des unités et du quotient.

Il est facile de conclure de ce qui précède que tous les problèmes d’arithmétique peuvent être résolus au moyen de la machine ; et que, dans les calculs compliqués, elle doit apporter une rigoureuse exactitude et une grande célérité.

L’invention de M. le chevalier Thomas nous paraît devoir être rangée au nombre de ces découvertes qui font honneur à ceux qui les conçoivent, et sont glorieuses pour l époque qui les produit. » 

www.arithmometre.org
2013