En quête de l'entier quotient d'une division ...
I) Le "mémento"
L'idée de donner à l'arithmomètre de Mr Thomas, "la propriété d'écrire dans des lucarnes spéciales l'entier quotient d'une division" est mentionnée dans un rapport de Benoît, en date de mars 1851, et rédigé dans le célèbre "Bulletin de la Société d'encouragement pour l'industrie Nationale" (BSEIN).
Cette courte mention fait suite à la description détaillée de l'arithmomètre T1850, qui rappelons-le, possède un index multiplicateur. Cet indicateur de tours, ou index, permet de lire, dans le cas d'une division, le quotient partiel. Dans le cas d'une opération complexe, l'opérateur va devoir noter ces quotients partiels s'il veut, au final, obtenir l'entier quotient de la division.
L'idée de créer des lucarnes spéciales est donc intéressante !
Parfait !
Mais de quoi parle t'il réellement ici ?
En fait, le texte de Benoît est peu précis sur ce sujet. Rien n' indique clairement qu'on soit en présence d'un système mécanique en relation avec la manivelle motrice !
Ne ferait-il pas plutôt allusion à ces lucarnes nommées "Mémento" que l'on trouve sur les machines à 8 chiffres de l'époque !
S'il est possible en effet d'y noter les résultats intermédiaires, et pourquoi pas l'entier quotient d'une division, ce système ne comptabilise rien mécaniquement ! C'est l'opérateur qui place ses valeurs sur ce "Mémento".
Attention ! ne confondons pas ! Ce n'est pas un compteur de tours !
NB : Benoît parle de l’entier quotient, ce que nous avons repris dans notre titre de page, mais il faut bien noter que les machines comportent toutes la possibilité de placer une cheville d’ivoire entre les différentes lucarnes, ce qui permet de matérialiser la place d’une éventuelle virgule. Il est donc tout à fait possible de pousser la division au-delà de l’entier quotient, afin d’avoir des décimales.
|
 |
Le "mémento" à 8 fenêtres est placé sur la platine fixe de l'arithmomètre, à gauche.
Il n'y a aucune relation avec la manivelle motrice
|
T1850 B (détail) |
 |
L'opérateur inscrit manuellement les multiplicateurs ou les quotients partiels ! |
II) Des cadrans pour les quotients
En août 1851, Thomas de Colmar dépose un certificat d'addition au brevet de 1850, portant sur un "perfectionnement qui aura pour effet de faire paraître le quotient dans la division, et le produit dans la multiplication". L'idée de Benoît a fait du chemin ...
On est en présence ici d'un vrai système mécanique en relation avec la manivelle motrice !
On a placé à la suite du premier cylindre de droite une pièce cylindrique dont la forme étudiée permet de donner à un levier un mouvement de va et vient. Ce levier est lui-même relié à une sorte de fourchette dont les deux bras qui la composent auront pour effet de faire tourner une roue dentée (pignon) dans un sens ou dans l'autre, selon que l'on procèdera à une Addition/ Multiplication ou à une Soustraction/Division.
Ce "pignon" est tout petit de manière à ne pas gêner le fonctionnement des grandes roues totalisatrices. Il communique avec une aiguille qui est placée sur la platine et qui va marquer sur un "cadran" à double rangée de chiffres, le nombre de tours de manivelle que l'on fait. On l'a bien compris ! ce "cadran" est gravé sur la platine ! ce n'est pas un cadran mobile ! C'est l'aiguille qui va indiquer la valeur du quotient partiel. Et comme on a adapté à la platine des cadrans autant de roues (pignons) qu'il y a de cylindres dans la machine, "la même fourchette agira successivement sur ces différentes roues, suivant qu'on les mettra en communication, en portant la platine (déplaçant) vers la droite ou vers la gauche". On aura donc ainsi l'entier quotient de la division !
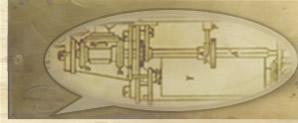
Certificat d'addition d'Août 1851 (détail)
|
|
|
Détail du brevet imprimé !!!
|
|
| |
Détail du brevet manuscrit !!!
.... L'aiguille du cadran ... |
|
Remarques :
Malheureusement, nous n'avons jamais retrouvé de machines T1850, ni même T1852, dotées du mécanisme décrit dans le certificat d'addition du 19 août 1851 !
L'erreur serait d'attribuer à S/n 11 et S/n 16 ce privilège sous prétexte qu'ils ont des numéros de série très bas et qu'ils sont dotés de lucarnes de quotient. Mais un petit numéro de série n'est pas une preuve d'antériorité en soi (cf. L'épopée des numéros de série). D'autre part, ils possèdent de vraies lucarnes de quotient, ce qui n'est pas le cas dans notre certificat d'addition !!
Ici, il n'y a pas de lucarne !! et pas de cadran mobile ! on a un pignon relié à une aiguille qui vient pointer vers un des valeurs du multiplicateur ou du quotient. C'est un peu comme un cadran de montre finalement ! Ce ne sont pas les chiffres qui tournent mais c'est l'aiguille !
On ignore pourquoi ce système ne fut pas généralisé sur l'ensemble des machines car cela constituait tout de même une innovation importante par rapport à l'index multiplicateur, qui, lui, ne donnait que des quotients partiels. Moigno, en février 1854, indique que « la pratique a prouvé que les indicateurs de tours et les cadrans des chiffres du quotient n'étaient ni indispensables ni même véritablement utiles ; que l'obligation de compter les tours, imposée à l'opérateur, ne lui donnait, en réalité, aucune peine et n'était pas une source d'erreur; on les a donc supprimés.»
III) Le piano-arithmomètre de l'exposition universelle de 1855
En 1855, à l'Exposition universelle de Paris, Thomas de Colmar sort le grand jeu ! Il y présente un arithmomètre géant aux allures de piano. La machine est impressionnante ! Le meuble, peut-être construit par Tahan, est à lui seul un petit bijou !
La machine a une capacité de 30 chiffres, ce qui est exceptionnel à l'époque.
Elle fit tant impression qu'elle en marqua l’esprit même
de Jules Verne dans un de ses romans visionnaires écrit en 1863 :
« Paris au XXe siècle ».
Le piano arithmomètre de 1855 |
Vue de la platine mobile |
|
|
Extrait :
« … Pour commencer votre
apprentissage, vous serez attaché à la machine N° 4. Michel se
retourna et aperçut la machine N° 4. C’était un appareil à calculer.
Il y avait loin du temps où Pascal construisait un instrument de
cette sorte, dont la conception parut si merveilleuse alors. Depuis
cette époque, l’architecte Stanhope, Thomas de Colmar, Maurel et
Jayet, apportèrent d’heureuses modifications à ce genre d’appareils.
La maison Casmondage possédait de véritables chefs-d’œuvre ; ses
instruments ressemblaient, en effet, à de vastes pianos ; en
pressant les touches d’un clavier, on obtenait instantanément des
totaux, des restes, des produits, des quotients …..on le voit, il
entrait dans une maison de banque qui appelait à son aide et
adoptait toutes les ressources de la mécanique. D’ailleurs, à cette
époque, l’abondance des affaires, la multiplicité des
correspondances, donna aux simples fournitures de bureau une
importance extraordinaire. » / Jules Verne
La communauté scientifique est enthousiaste !
L'Abbé Moigno, toujours lui ! écrit, en Juillet 1855, un bel article dans la revue Cosmos sur « l'arithmomètre géant de M. Thomas de Colmar, N° 1088 du catalogue, nef centrale du Grand Palais, près du phare de l'administration » :
"Ce que nous trouvons de plus remarquable dans l'apparition de l'Arithmomètre géant de l' Exposition universelle, c'est qu'alors qu'il semblait extrêmement difficile de lui faire réaliser tous les avantages des petites machines plus faciles à construire, M. Thomas de Colmar ait osé aborder des perfectionnements nouveaux.
Ainsi, les nombres de tours de manivelle se montrent dans des lucarnes spéciales, et comme ces nombres sont toujours plus petits que 9, ils se montrent tels qu'ils se sont produits dans les multiplications et les divisions partielles successives, de sorte qu'après la multiplication faite, la série de ces nombres représente le multiplicateur et devient, par sa seule présence, un témoin authentique, une preuve irrécusable de la vérité, de la bonté de l'opération ; qu'après la division achevée, il donne le quotient, sans qu'on ait eu besoin d'enregistrer à part ses chiffres successifs, à mesure qu'ils ont été obtenus." / Cosmos, 13 juillet 1855, page 44
Et oui ! On y revient ! Souvenez-vous ! 17 mois plus tôt, en Février 1854, notre cher Moigno nous disait que c'était inutile !
L'expérience a montré que cela simplifiait tout de même les procédures de calcul. La présence de compteurs à chaque ordre décimal permet d'obtenir le multiplicateur ou le quotient sans avoir à prendre de notes, ce qui "enlève à l'opérateur, toute préoccupation et lui permet d'effectuer, sans contention d'esprit, les calculs les plus compliqués" Sébert, 1879
B) L'introduction des lucarnes de quotient sur les modèles de série (1858)
Vers 1858, Thomas intègre le principe sur ses modèles de série. Techniquement, ce n'était pas si facile à faire, car le chariot était déjà plein de rouages et de ressorts !
Pour ranger tout ce beau monde sans modifier la taille de sa machine, notre inventeur dut augmenter l'épaisseur de la plaque du chariot et travailler sur plusieurs couches. De la sorte, les pièces pouvaient se chevaucher partiellement sans se gêner dans leurs fonctions respectives !
Notons ici que la datation reste difficile car on ne dispose que de très peu de documents couvrant la période 1856-1862 . Il est communément admis dans la littérature que 1858 correspond à la date d'introduction des lucarnes de quotient sur les modèles de série. Quand on essaye de remonter à la source bibliographique, c'est dans un texte de Sébert, daté de 1879 que l'on trouve l'information.
« ... C'est ce perfectionnement qui se trouve dans les machines actuelles; il n'a, d'ailleurs, été réalisé que vers l'année 1858, et de la façon suivante. Sous chaque lucarne du petit compteur, existe un cadran indépendant, monté sur une roue dentée de 18 dents. Chaque cadran porte, à droite et à gauche, la série de chiffres 1,2,3 etc., jusqu'à 9, le chiffre 9 étant commun aux deux séries.
Chaque roue dentée, lorsqu'on déplace la platine mobile, vient, à son tour, engrener avec une roue qui se meut, tantôt dans un sens, tantôt dans l'autre, suivant le sens de la marche de la machine et qui avance d'une dent à chaque tour de manivelle. Chaque cadran indique donc le nombre de tours faits par la manivelle, en tenant compte du rang des unités sur lesquelles on opère, mais ne peut marquer plus de 9 tours, à moins de décompter après le neuvième.» / BSEIN, 1879, pages 404-405
Modèle T1858 |
S/n 16 |
|
| |
Modèle T1860 |
S/n 52 |
|
|
Modèle T1865 |
|
|