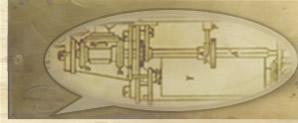
Mise à jour Mars 2013

I) La roue multiplicatrice T1820

La roue multiplicatrice est tout simplement un compteur de tours à un chiffre. Rappelons que sur ces machines, la multiplication n'est pas directe. Elle s'opère par somme d'additions. 282 x 7, c'est 282 + 282 + 282 + ... (7 fois). A chaque tour de cylindres, le multiplicande inscrit par l'opérateur est rajouté au totalisateur. Il peut donc s'avérer très utile de contrôler le nombre de rotations pour éviter toute erreur dans le résultat. Pour être plus précis, on pourrait dire que la roue T1820 est un décompteur de tours. En effet, pour chaque chiffre du multiplicateur, l'opérateur doit placer une cheville dans l'un des dix trous correspondant (0,1,2,3,4,5,6,7,8 ou 9). A chaque rotation des cylindres, un"'doigt", placé sous la roue, la fait avancer d'un cran. Lorsque le multiplicateur est atteint, la cheville vient buter sur un arrêt et la machine est stoppée. Il y a donc une volonté de sécuriser l'opération. Pour un multiplicateur à plusieurs chiffres (x27 par exemple), il convient, après avoir décaler le "chariot" totalisateur d''un rang décimal, de replacer la cheville dans le trou correspondant au second chiffre du multiplicateur.

En fait, la machine se comporte comme si l'on posait une opération sur le papier, à la différence qu'ici, l'esprit est mécanisé..

La multiplication 282 x 27, posée sur le papier	La multiplication 282 x 27, sur T1820 1er chiffre du multiplicateur
	2ème chiffre du multiplicateur

L'emploi d'un multiplicateur/compteur à un chiffre n'est pas dramatique en soi pour une multiplication. C'est juste que l'opérateur ne doit pas s'emmêler les pinceaux si le multiplicateur est à 4 chiffres. Ce qui est plus gênant, c'est pour la division, qui est une somme de soustractions. Rappelons que sur T1820, il n'y a pas de réversibilité des totalisateurs, et c'est en employant la numérotation complémentaire, que l'on peut effectuer cette opération. Quoiqu'il en soit c'est le compteur qui ici va nous fournir le quotient. Il va falloir donc s'armer d'un stylo pour noter un à un les quotients partiels.

Divisons 7614 par 282.
On écrit le nombre 7614 sur les cadrans du totalisateur (en mode numérotation complémentaire) et le diviseur 282 en déplaçant les curseurs de l'inscipteur sur 2, 8 et 2. On décale ensuite le chariot de manière à présenter le premier dividende partiel 761 au dessus de 282. En fait c'est comme si on voulait savoir combien de fois retrancher 282 à 761. Il y a deux façons de procéder. On peut placer la cheville dans le trou de la roue marquant le chiffre 1 et on tire le cordon (=1 rotation des cylindres). La différence, 479, s'affiche alors dans les cadrans. Si cette somme est supérieure au diviseur, on recommence la procédure, jusqu'à ce que la différence soit inférieure au diviseur. Dans le cas ici présent, on peut soustraire 2 fois 282 à 761 et il reste 197. On aurait pu aussi voir la chose du "premier coup d'oeil" et anticiper en mettant la cheville directement dans le trou marquant le chiffre 2, ce qui, en tirant le cordon, aurait fait faire directement deux tours aux cylindres. Mais cela nécessite déjà des qualités cognitives...
Le reste étant plus petit que le diviseur, on décale le chariot d'un rang décimal, de manière à présenter le second dividende partiel 974 au dessus du diviseur. Cela revient à se demander combient de fois je vais pouvoir retrancher 282 à 1974. Rebelotte, on recommence la procédure, soit pas à pas, soit en utilisant ses qualités cognitives. Le quotient donnera 27, avec un reste de 0.

On voit bien qu'avec un compteur de tours à un chiffre, on est obligé de noter les un à un les quotients partiels, ce qui est assez contraignant, reconnaissons-le !

II) Thomas vs Leibniz

Parmi les machines des 16ème et 17ème siècles, la machine de Leibniz est celle qui présente le plus de similitudes avec l’arithmomètre de 1820. On en arrive vite à se poser la question de savoir si Thomas de Colmar eut connaissance des travaux de Leibniz.  Il aurait pu, dans les années 1816 à 1819, aller voir et étudier la machine conservée à Gottingen, en Allemagne. Cette ville était très universitaire et de nombreux savants français et étrangers y professaient. On peut aussi penser que Thomas a étudié l’histoire du calcul mécanique en se servant tout simplement des ressources disponibles dans les livres. Il a très bien pu lire les écrits de Leibniz ou de Leupold pour en extraire la substantifique moelle.

Au nombre des similitudes, nous pourrions citer :

Cela fait donc beaucoup de hasards ... Mais je laisse le lecteur se faire sa propre opinion.

Roue T1820		Roue de Leibniz (1694)

 II) Illustrations

La roue multiplicatrice T1820 (le décompteur de tours)
	On voit en noir les trous destinés à recevoir la cheville g et en blanc les 10 chevilles f qui se situent en dessous de la roue. Le bras h maintient la roue et sert de butoir à la cheville g lorsque la valeur du chiffre du multiplicateur est atteinte.

Vue latérale de la roue
	Les 10 chevilles f  (ici 5 seulement sont visibles) servent à faire tourner la roue.

Plan en coupe de la roue et de la dent o

A chaque rotation la dent o, en poussant une cheville f, fait tourner la roue d’un dixième de tour.

Vue supérieure du mécanisme et de la dent o

www.arithmometre.org
2013