* Translation and adaptation by Michel Bardel, France

The quotient quest…

I) The "memento"

The idea to give the arithmometre “the property to display the integer(*) quotient of a division in special windows” is mentioned in a report from Benoît, dated march 1851. It is published in the well-known "Bulletin de la Société d'Encouragement pour l'Industrie Nationale" (BSEIN).

This short mention follows a detailed description of the T1850 arithmometre, which, let us remind it, already incorporates the multiplier/quotient cursor. This counter gives, one after the other, the digits of a quotient. For a long quotient, the operator has to remember or to note these digits to get the final quotient.

The idea to design a special window is therefore important. Perfect ! But what kind of window ?

In fact Benoît’s text is not precise enough. Nothing clearly shows that the windows have to be linked in any way to the driving mechanism. It could well be a row of independent windows, called “memento” on the eight digit machines of this period.
These windows are only used to note the intermediate digits of a quotient. They are manually set by the operator after the cursor digit.
So be careful, this row of windows is NOT a counter.

(*) Benoît improperly used the expression “integer quotient”. It must be noted that all the arithmometres since xxxx display a row of pin holes between the dials. An ivory pin can be placed at will, to materialize the position of a decimal point. It was therefore as easy to compute a decimal quotient than an integer one. Benoît was certainly aware of that. Does that mean that Benoît meant “entire quotient”, therefore thinking of a genuine counter ?

T1850 B

The 8 window “memento” is located on the fixed plate, on the left side. There is no mechanical link with the driving mechanism.

T1850 B (détail)

The operator sets each multiplier or quotient digit himself.

II) The multi-pointer counter

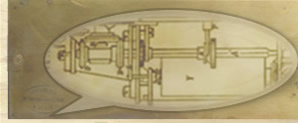
In August 1851, Thomas files an addition to his 1850 patent, teaching an “improvement the benefit of which is to display the quotient in a division, and the multiplier in a multiplication”. Benoît’s idea is on its way… We are now facing a real mechanical system, linked to the driving mechanism.

Linked to the first stepped drum, a cam gives a lever a reciprocating movement. This lever is linked to a fork. Depending on the operation performed (multiplication or division), one or the other hand of this fork makes a gear advance by one tooth, clockwise or anticlockwise.

This counter gear is small enough to be inserted under the carriage plate without disturbing the total dials. It is linked to the axis of a pointer, placed above the plate, pointing the number of crank turns to a dual graduation engraved in the plate. As we have as many counter gears as total dials, “the same fork will successively act on these gears as we move the carriage to the right or to the left”. The entire quotient (or multiplier) will show at the end of the operation. Thomas has achieved the first proper counter.

Addition certificate August 1851 (details)

Printed patent detail

Manuscript patent detail !!! The pointer

Remarks:

We have never found any machine T1850, nor T1852, having a counter as described in the addition certificate of August 19th, 1851. We tend to think that it was never manufactured.

We don’t know why this counter was not manufactured, as it was a real breakthrough compared to the previous one digit systems.

Moigno, in February 1854, tells us that “ practice proved that one digit counters are not essential, not even useful ; the duty of counting turns doesn’t really bother the operator, and is not causing errors ; so they were removed.”

III) The counter

A) The piano-arithmometre of the International Exhibition of 1855)

In 1855, at Paris International Exhibition, Thomas plays the big game!
He presents a gigantic arithmometre looking like a piano. The machine is impressive, and the case, probably built by Tahan, is, in itself, a pure jewel.
The machine capacity is 30 digits. It is so impressive that it has a big impact on Jules Verne’s mind, as can be seen in its visionary novel : « Paris au XXe siècle », (Paris in the 20th century), written in 1863.

The piano-arithmometre of 1855	The carriage plate

Extract :

« "…To begin your apprenticeship you will work on machine number four. Michael turned and saw machine number four. It was a calculating machine.  It had been a long time since Pascal built such a machine whose conception seemed so amazing then.  Since then, the architect Stanhope, Thomas de Colmar, Maurel and Jayet had introduced useful modifications to this type of machine.  Casmondage owned some true masterpieces; the machines resembled enormous pianos; on pressing the keys, one immediately obtained totals, remainders, products or quotients…..it was evident, he was joining a bank which required, and adopted, all possible mechanical help.  Besides, at this time, the volume of business and the quantity of correspondence, gave an extraordinary importance to ordinary office equipment." » / Jules Verne

The scientific community is enthusiastic! In July 1855, the abbot Moigno writes a beautiful article in the review Cosmos about “Mr Thomas de Colmar’s gigantic arithmometre, #1088 in the catalogue, Grand Palace central nave, next to the administration lighthouse” :

“What we find most remarkable in the outbreak of the gigantic arithmometre is that Mr Thomas de Colmar dared to address new improvements, where it seemed to be already extremely difficult to achieve all the advantages of smaller machines, much easier to build.
“Thus, the numbers of crank turns show in special windows, and, as these numbers are always smaller than nine, they show just as they are produced in the successive partial multiplications and divisions, so that after the multiplication is done, the block of numbers represent the multiplier and becomes, by it own presence, an authentic witness, an unimpeachable proof of the operation truth and accuracy ; after the division is done, it gives the quotient, without any need for recording its successive digits on the side, as they are obtained.” Cosmos, July 13, 1855, page 44

So, yes! We are back to it! Remember! Seventeenth months earlier, in February 1854, the same Moigno was pleading that counters were useless!
It is true to say that this new kind of counter is much more efficient and makes the difference.
As Sebert says, the counter “relieves the operator of all concern, and gives him the possibility to perform the most difficult calculations without any mental strain”. Sébert, 1879

B) The counter on serial production (around 1858)

Around 1858, Thomas adopts the counter on his serial models. Technically, it is not an easy task, because the carriage is already full of gears and springs.

To pack up all this beau-monde without altering the machine size, the inventor had to increase the carriage plate sickness, and work on several layers. Like this, the piece parts can partially overlap without any drawback in their respective functions.

It is important to note that it is difficult to assign a date to this improvement, because we dramatically lack documents covering the 1856-1862 period of time.
It is commonly accepted, in our bibliography, that 1858 is the year of introduction of the “quotient windows” (counter) on serial models. All these references rely on the same and only Sebert’s text dated 1879 :

“… It is this improvement that you can find in present machines; incidentally, it was only achieved around 1858, and as follows. Under each window of the small counter, is a small dial, mounted on an 18 tooth gear. Each dial bears, on the left as on the right, a series of digits 1, 2, 3, etc., up to 9, the digit 9 being common to both series. Each gear, when the carriage is moved, comes into gear with another gear that turns, sometimes in one direction, sometimes in the other, function of the operation being made, and that moves one tooth per crank turn.
Each dial therefore shows the number of turns made by the crank, taking care of the decimal place on which one operates, but can’t show more than nine, or it counts down after the nine turn.” / BSEIN, 1879, pages 404-405

T1858 model

S/n 16

T1860 model

S/n 52

T1865 model