Mise à jour Mars 2013

I) Principe de la numérotation complémentaire

C'est la solution initiale trouvée par Pascal pour que sa machine puisse effectuer des soustractions/divisions. La raison est mécanique : le mécanisme de retenue n'est pas réversible. L'opérateur ne peut tourner les roues en sens inverse pour soustraire au totalisateur la valeur inscrite sur l'inscripteur. La "méthode des compléments" permet de contourner le problème en remplaçant la soustraction par une simple addition. On utilise pour cela le complément d’un nombre (la somme d’un chiffre et de son complément doit être égale à 9). Par exemple, le complément de 89057 est 10942.

Posons une soustraction  :

243-125 = ?
Le complément de 243 est 756  [(2+7=9)(4+5=9)(3+6=9)]

La somme de 756+125 = 881
Le complément de 881 est 118

243-125 = 118

Pour éviter d'avoir à calculer systématiquement le complément d'un nombre, chaque cadran du totalisateur possède une double numérotation. Une fenêtre laisse apparaître un chiffre, et à côté, une autre fenêtre donne son complément. Il suffit alors d'occulter l'une ou l'autre des fenêtres, pour opérer une addition/multiplication ou une soustraction/division.

La Pascaline (1645)

On retrouve ce dispositif sur de nombreuses machines à calculer du 18ème siècle. Les machines de Gersten, Braun, Hahn, Schuster, et Muller possèdent toutes ce double affichage.

Machine de Hahn & Schuster (Circa 1780)

La machine de Leibniz possède en revanche un reporteur réversible. Son totalisateur affiche une numérotation simple. Signalons au passage que tout cela ne fonctionnait pas très bien, en particulier dans la gestion des retenues en cascade (999+1). Si la première retenue fonctionnait, la deuxième (décade n+1) n'avait pas le temps de passer. 99+1 donnait 000. Pour plus de détails, je vous invite à lire l'article qui lui est consacré (Voir en page d'accueil).

Multiplicatrice de Leibniz

II) Numérotation complémentaire sur T1820 et T1822

a) De la non réversibilité du reporteur

La non réversibilité du reporteur des arithmomètres T1820 et T1822 a plusieurs causes.

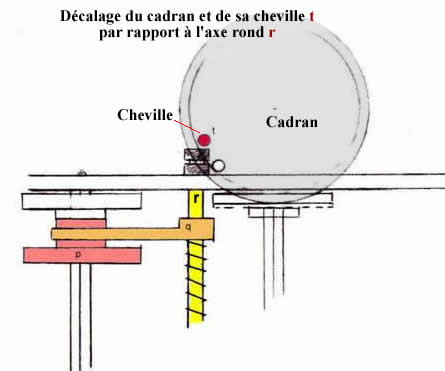
T1820
Au passage de 9 à 0 d'un des cadrans du totalisateur, une cheville placée sous le cadran vient pousser horizontalement un axe rond monté sur ressort à boudin. Pour que cela soit possible, il faut obligatoirement que le cadran soit décalé par rapport à cet axe, ce qui lui permet aussi de s'échapper. Dans cette configuration, il est impossible que le cadran tourne dans l'autre sens, sans quoi la cheville ne pourrait plus pousser l'axe rond. On va dire que c'est rédhibitoire ! Même si les cylindres pouvaient tourner dans les deux sens, le totalisateur, lui, ne suivrait pas.

T1822
Le problème sur T1822 est différent. La pression qu'exerce le plan incliné sur le cliquet est verticale. L'extrémité supérieure du cliquet se situant dans l'axe médian du cadran, rien ne s'oppose à ce que le plan incliné fasse son office sur le cliquet quelque soit le sens de rotation.

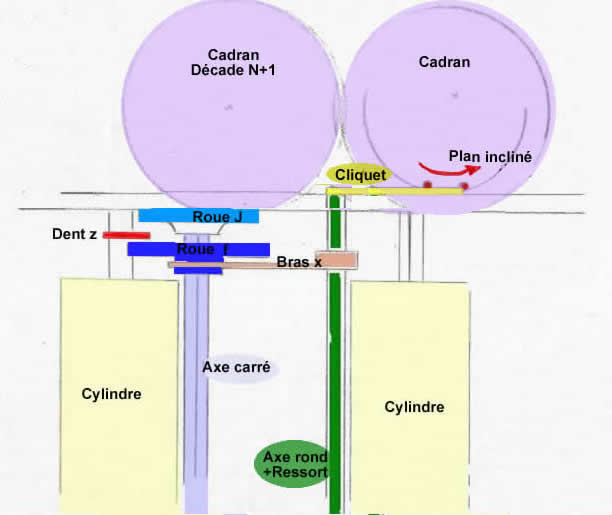
C'est le positionnement de la dent de retenue qui rend l'histoire impossible. Rappelons que celle-ci est décalée angulairement par rapport aux 9 dents du cylindre. Pour un rang décimal donné, une retenue ne peut être transmise au rang décimal supérieur qu'après que le chiffre inscrit par l'opérateur ait été transmis au totalisateur. C'est la position du plan incliné placé sous le cadran qui amorce cette retenue. Mais ce n'est pas tout ! Afin qu''une éventuelle unité de retenue en provenance du rang décimal inférieur (N-1) puisse être prise en compte , il faut que les cylindres soient décalés d'un vingtième de tour les uns par rapport aux autres, sans quoi toute retenue en cascade serait impossible (99999+1 par exemple). La partie non dentée du cylindre, qui occupe les 11/20 ème, permet justement de gérer ce train de retenues (aussi appelé "Pont de report).
Si l'on décide d'inverser le sens des cylindres, non seulement cette zone vierge va passer en premier, ce qui est aberrant, puisque aucun chiffre n'a encore été transmis au totalisateur, mais de plus, la dent de retenue va passer avant les autres ! Aucune retenue ne peut alors s'effectuer.
Et puis pour corser le tout, la rampe hélicoïdale a (Colimaçon) ne peut fonctionner que dans un sens. Sa pente progressive repositionne la roue de retenue f en position neutre (grace au double bras xy). En rotation inverse il y aurrait blocage immédiat.

 

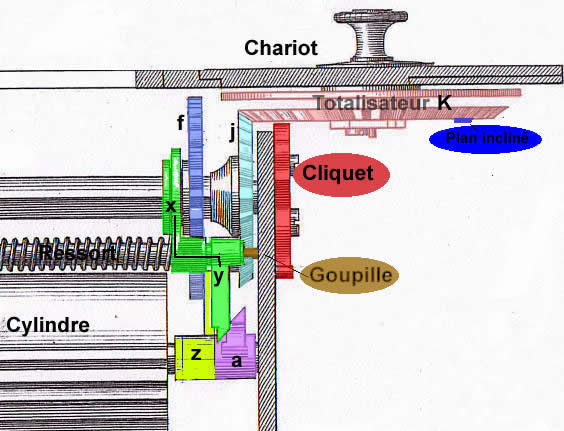
Voilà en quelques mots les contraintes techniques qui ont sans doute amené Thomas a abandonner l'idée de la réversibilité des cylindres. Notons qu'à cette époque, il n'avait pas encore pensé à intégrer un inverseur de marche sous le totalisateur, ce qui permettait de changer le sens de rotation des cadrans, sans changer le sens de rotation des cylindres. IL faudra attendre 1848 pour cela.

b) Cadrans et fenêtres

Sur T1820 et T1822, chaque cadran porte deux séries de chiffres. C'est la numérotation complémentaire. La première série (en rose) sert pour les opérations d'addition et de multiplication (qui est une somme d'additions). On notera qu'elle a été doublée afin de donner au cadran un diamètre suffisant. La conséquence directe est que sous chaque cadran il n'y a pas une, mais deux chevilles sur T1820 (deux plans inclinés sur T1822). La seconde série (en bleu) sert pour les opérations de soustraction et de division (qui est une somme de soustractions).

 

 

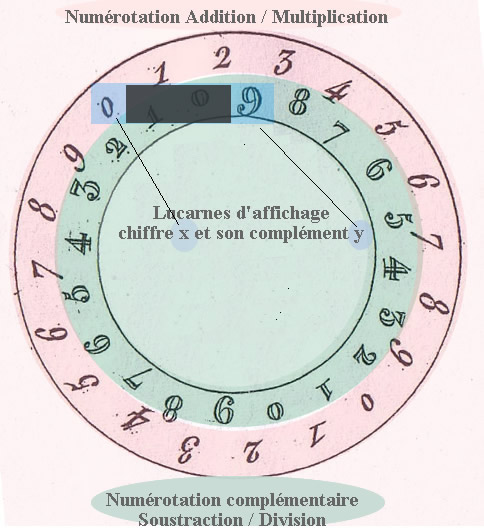
Au niveau de l'affichage, une fenêtre laisse apparaître un chiffre, et à côté, une autre fenêtre donne son complément. Elles sont rondes et bien séparées sur T1822. Sur T1820 on occulte l'une ou l'autre des fenêtres en tirant sur sur réglette plate.

 

 

Arithmomètre 1820 (dessin)

www.arithmometre.org
2013