Mise à jour Mars 2013

I) Pascal vs Leibniz : de l'additionneur au multiplicateur ...

Blaise Pascal (17) est né le 19 juin 1623 à Clermont Ferrand. Sa mère meurt quand il a 3 ans. C’est son père, passionné de mathématiques et de sciences qui fera son éducation.  Ils montent à Paris en 1631, puis en 1639, s’installent à Rouen.
Son père devient commissaire député pour la levée des impôts en Haute Normandie. Accablé par d’incessants calculs administratifs et comptables, Blaise développe l’idée de construire une machine arithmétique pour alléger la charge de travail de son père.
En 1645, après 3 ans de recherches et d’essais, il construit la première machine arithmétique fonctionnelle, avec report automatique des retenues !! Pascal n’est âgé alors que de 22 ans ! 8 exemplaires de la machine arithmétique de Pascal sont connus,  plus une, tardive, qui fut reconstruite au 18e siècle à partir de pièces originales. La machine coûte cher, au moins 100 livres de l’époque, soit 3 mois d’un salaire vraiment confortable(18).

Description rapide  de la machine
La machine se présente sous la forme d’un caisson dans lequel est renfermé le mécanisme et d’une platine supérieure qui se décompose en deux parties principales : l’inscripteur et le totalisateur.(19)
L’inscripteur permet à l’opérateur de poser le nombre à additionner ou à soustraire. Il est composé d’une série de roues étoilées montées sur des axes indépendants, et qui correspondent à un ordre décimal ou monétaire. Chaque roue de l’inscripteur fonctionne un peu comme un cadran de téléphone : le limbe et le butoir sont solidaires du bâti, la roue étoilée est mobile. Pour inscrire un chiffre, l’opérateur place son stylet entre 2 rayons, et tourne la roue jusqu’à ce que le stylet soit arrêté par le butoir. Un rayon correspond à une unité de l’ordre décimal ou monétaire choisi. Pour les deniers, on aura des roues à  12 rayons, pour les sols des roues à 20 rayons,  et pour le système décimal classique, des roues à dix rayons ! La rotation de la roue va entrainer le mécanisme. Celui-ci est plutôt simple. On y retrouve des roues à chevilles (20), qui assurent la transmission des données au totalisateur, des cliquets, qui permettent aux différentes roues de bien se positionner,  et des sautoirs, dont la mission est de transmettre la retenue à l’ordre décimal supérieur.

C’est donc avec Pascal que commence véritablement l’Histoire du calcul mécanique. On a une machine comportant  une « Interface utilisateur » fonctionnelle, à savoir :

• Un inscripteur
• Un totalisateur
• Et puis un mécanisme de report automatique des retenues qui va libérer l’esprit de l’homme, ou pour reprendre l’expression de Pascal  « animer le cuivre et donner l’esprit à l’airain ».

Au niveau de ses performances, même si elle est capable d’effectuer les quatre opérations de l’arithmétique, elle est beaucoup moins rapide pour les multiplications ou les divisions. C'est possible bien sur, mais par additions ou soustractions répétées.

492 x 9
C’est 492  + 492  + 492  + 492   répétés 9 fois !!
L’opérateur doit réinscrire à chaque fois le multiplicande autant de fois que c’est nécessaire. Il y a donc une contrainte qui peut être source d’erreur….

Il faudra attendre quelques dizaines d’années (1694) pour qu’un autre inventeur de talent, Leibniz,  invente la première multiplicatrice de l’Histoire (22). Docteur en droit, philosophe, mathématicien, Leibniz est un homme aux multiples facettes. Son trait de génie a été de séparer physiquement le totalisateur de l’inscripteur (23). Sur la machine de Pascal, ce n’était pas le cas, les deux étaient en prise directe : la rotation de la roue étoilée provoquant immédiatement l’avancée du totalisateur. Ici, il y a une phase intermédiaire. On pose d’abord le multiplicande à l’aide d’index rotatifs qui sont gradués de 0 à 9, puis on tourne une manivelle. A chaque tour de manivelle, le multiplicande est rajouté au totalisateur.

Cela parait anodin mais l’intérêt est double :

• D’une part, l’opérateur n’a plus besoin  de réinscrire à chaque fois les chiffres du multiplicande comme cela devait se faire sur la machine de Pascal.
• D’autre part en décalant à volonté le multiplicande par rapport au totalisateur, il devient possible d’effectuer rapidement des opérations avec un multiplicateur à plusieurs chiffres, un peu comme on le fait quand on pose une multiplication sur le papier.

La différence est fondamentale !!

Le système mécanique qui permet de transmettre le multiplicande au totalisateur s’appelle l’entraîneur. L’organe principal qui le compose, c’est le cylindre denté, dit aussi cylindre de Leibniz (24) car il est à l’origine d’une longue lignée de machines à calculer dont l’arithmomètre en est évidemment l’exemple même.

Alors comment ça fonctionne ?

Le cylindre porte au niveau de sa circonférence neuf dents de longueurs croissantes. Elles suivent une progression arithmétique allant de 1 à 9. Lorsque l’opérateur tourne les index rotatifs, il provoque le déplacement horizontal de ces cylindres. Pour chaque chiffre posé, on a un cylindre qui vient se positionner sous un pignon qui est monté sur l’axe communiquant avec le totalisateur. Lorsqu’on tourne la manivelle, le cylindre effectue une rotation de 360° et met alors en prise un certain nombre de ses dents avec le pignon. Le nombre de dents rencontrées équivaut tout simplement à la valeur du chiffre posé ! Pour le chiffre 1, une dent. Pour le chiffre 2, deux dents et ainsi de suite. Le cylindre est donc l’organe reproducteur la multiplicatrice de Leibniz.
Malheureusement la machine de Leibniz marchait plutôt mal. Malgré les sommes investies, environ 10000 florins, son mécanisme de retenue défaillait lors des retenues en cascade. Par exemple 96 + 4 ne donnait pas 100 comme il se devrait mais 000 ! Un système de roues dodécagonales indiquait à l'opérateur où la retenue n'était pas passée. Il lui fallait alors remettre les inscripteurs à zéro et refaire un tour de manivelle pour terminer le processus.

2) Les autres types d'entraîneurs

Au 18ème siècle, différents types d'entraineurs seront mis au point. Nous citerons les deux principaux :

a) L'entraîneur à nombre variable de dents de Poleni (1709)

Joannis Poleni est un homme de science italien, qui succéda à Nicolas Bernoulli à la chaire de mathématiques de l’université de Venise. Il a inventé en 1709 une machine arithmétique (29) qui ressemble un peu aux horloges en bois de la forêt noire. Son mécanisme était entraîné par des poids, ce qui est une idée intéressante, puisque cela permet d’automatiser dans une certaine mesure le calcul. Son entraîneur est différent de celui de Leibniz.  C’est un entraîneur dit à nombre variable de dents. Pour se représenter la chose, il suffit d’imaginer un disque un peu épais comportant au niveau de la circonférence des dents rétractables. Lorsque l’opérateur inscrit un chiffre, un mécanisme fait sortir les dents ! Une dent, deux dents, trois dents, jusqu’à neuf dents ! Le poids fait tourner le disque et les dents engrènent avec les roues du totalisateur. Je vais vous raconter une petite anecdote au sujet de Poleni. Non loin de là, à Vienne, un habile mécanicien et fabricant d’instruments d’optique et de mathématiques, nommé Antonius Braun, construisit une machine arithmétique (30) absolument magnifique qu’il dédia à l’empereur Charles VI, et pour laquelle il reçut une récompense de 10000 florins. Poleni, quand il a vu ça, il y a un bout de bois qui lui est resté coincé dans le gosier !! Il faut dire que la machine est une pure merveille et techniquement elle est très aboutie. Comme chez Poleni, elle utilise le principe de l’entraîneur à dents mobiles, principe qui sera repris par Roth en 1840, par l’américain Baldwin en 1875 et surtout par le suédois Odhner en 1878. Alors !! que fit Poleni d’après vous ? Et bien, il  détruisit  sa propre machine et ne voulut plus jamais en entendre parler !! Quand au pauvre Braun, il mourut malheureusement très jeune d’une affection pulmonaire. Paix à son âme !!

b) L'entraîneur à contact intermittent de Leupold /Vayringe (1729/1750?)

Dans la lignée de Jean-Gaffin Gallon, Jacob Leupold rédige un énorme ouvrage de 7 volumes sur les techniques de l’époque : le Theatrum Machinarum. Dans son dernier volume, le « theatrum arithmetico-geometrum », une bonne partie est consacrée aux procédés de calcul, aux instruments et aux machines arithmétiques. On y retrouve la machine de Grillet, celle de Leibniz, de Poleni entre autres. Leupold décrit également deux de ses inventions, dont une machine arithmétique ressemblant dans sa forme à la machine de Braun, mais dont le mécanisme est différent (32). On n'a pas de trace de sa machine. Il est possible qu’il n’ait pas eu le temps de la fabriquer, la mort l’emportant en 1727, la même année que son dernier volume des Theatrum machinarum. Une magnifique réplique est visible au Heinz Nixdorf MuseumsForum, à Paderborn.
Quelques années plus tard, en 1750, Vayringe construisit une machine (33) reprenant le principe de l’entraîneur de Leupold. Le système est à la fois différent du cylindre de Leibniz et différent de l’entraîneur à nombres variables de dents que l’on retrouve sur la machine de Braun. C’est un entraîneur, dit « à contact intermittent ». Pour résumer, on a une crémaillère de 9 dents qui avance et recule devant chaque totalisateur. En fonction du chiffre inscrit par l’opérateur, la crémaillère restera en prise plus ou moins longtemps et transmettra jusqu’à 9 unités au totalisateur.

III) L'épopée du cylindre de Leibniz : Hahn, Schuster, Muller

Quoi qu'il en soit, le cylindre dit de Leibniz reste une valeur sûre. On le retrouve dans de nombreuses machines construites durant ce siècle des Lumières. Si sa forme varie, sa fonction reste la même, celle de reproducteur !

Leibniz (1694)	Hahn I (1770-1774)	Hahn II (1770-1776)
Schuster I (1789-1792)	Schuster II (1805-1820)	Schuster III (1820-1822)

IV) L'arithmomètre Thomas

Rappel : sur la platine fixe de l’arithmomètre, l’opérateur dispose de curseurs mobiles qu’il déplace librement afin de poser son multiplicande. Les curseurs sont reliés  par des fourchettes à des pignons qui coulissent sur des axes carrés, et qui vont, en fonction de leur position le long des cylindres, engrener sur un nombre adéquat de dents. Des pignons coniques montés sur ces mêmes axes transmettent au totalisateur le nombre posé par l’opérateur. L’opération se répète à chaque révolution des cylindres.

A) T1820

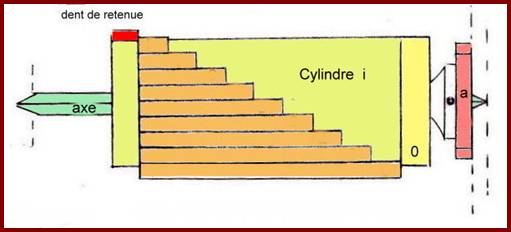
Dans le brevet de 1820, chaque cylindre possède 10 dents de longueurs inégales. Celles-ci occupent 10/14 de la circonférence totale. Elles ont été taillées de telle sorte que chacune perd 1/10e de sa longueur par rapport à la précédente. Seule les deux dernières, qui sont par ailleurs les plus petites, ont la même dimension. La logique voudrait que le cylindre ne possède que neuf dents, soit la valeur maximale d'un chiffre pour un rang décimal donné. Alors que fait cette dixième dent de trop ? Lorsque l’un des chiffres du totalisateur passe de 9 à 0, une cheville, placée sous le cadran concerné, provoque le déplacement d’une roue dentée et la place en position d’engrener avec cette dixième dent du cylindre. Sa fonction unique est donc de déclencher  la retenue. Elle est placée sur une tranche postérieure du cylindre afin de ne pas interagir avec les autres. A partir de 1822, cette dent "décalée" deviendra une dent "spécialisée" sitée après le cylindre, dans le prolongement de son axe.
La partie vierge du cylindre (4/14ème) sert pour la gestion des retenues en cascade ( par ex. 999+1). Pour que le report suscité par le passage à zéro du totalisateur de la décade n se produise, il faut que la roue de retenue de la décade n+1 tourne d'une dent. Pour se faire, il faut attendre que tout ce qui était à ajouter dans la décade n+1 l’ait été et qu'il ne reste plus que le report à faire. En conséquence la dent de report doit se trouver décalée angulairement par rapport aux autres dents du cylindre de la même décade. Ce report étant exécuté, il se peut que la roue totalisatrice de la décade n+1 soit passée de 9 à 0, ce qui nécessite un second report sur la décade n+2 (ex : 99+1=). Le cylindre de la décade n+2 doit être décalé en rotation d'au moins une dent par rapport au cylindre n+1, car si tel n’était pas le cas, la transmission de la retenue ne pourrait s’opérer à temps. C’est d’ailleurs le principal défaut de la machine de Leibniz qui ne gère pas ce type de retenue en cascade. L’arithmomètre T1820 possède 4 chiffres au multiplicande, donc 4 cylindres de type Leibniz. Le dernier cylindre sera décalé de 3 dents par rapport au premier. Il faut donc que la manivelle n'ait pas encore fini son tour quand le quatrième cylindre pose (éventuellement) son report. Les cylindres doivent donc avoir un espace sans dents correspondant au minimum au nombre de décades du registre de pose.

Coupe du cylindre T1820	Vue latérale

B) T1822

L'arithmomètre construit par l'horloger Devrine en 1822 a une particularité : les cylindres possèdent 18 dents. Pour être plus précis, chaque dent a été doublée. Quelle raison a poussé notre constructeur à modifier l'anatomie du cylindre ?

hypothèse:

Lorsque l'on compare ce modèle à celui de son ainé, T1820, on remarque immédiatement que le chariot est nettement plus large. L'inverseur de marche (Add./Mult -- Soustr./Div.) n'ayant pas encore été inventé, Thomas utilise pour l'affichage des résultats le principe des compléments, déjà employée par Pascal sur sa machine. Ce système permet tout simplement d'effectuer une soustraction en faisant une addition. On utilise pour cela le complément d’un nombre (la somme d’un chiffre et de son complément doit être égale à 9).

Prenons un exemple :

243-125 = ?
Le complément de 243 est 756  [(2+7=9)(4+5=9)(3+6=9)]

La somme de 756+125 = 881
Le complément de 881 est 118

243-125 = 118

Pour éviter d'avoir à calculer mentalement le complément d'un nombre, chaque cadran du totalisateur possède une double numérotation. Une fenêtre laisse apparaître un chiffre, et à côté, une autre fenêtre donne son complément. Il suffit alors d'occulter l'une ou l'autre des fenêtres, pour opérer une addition/multiplication ou une soustraction/division. On imagine sans peine que cela génère un contrainte de taille au niveau du diamètre des cadrans, ce qui pourrait avoir obligé Thomas a en construire de plus grands, et en conséquence, à doubler le nombre de dents sur les roues qui les portent (40 au lieu des 20 du brevet de 1820). Pour transmettre une unité au totalisateur, il faut désormais que la roue dentée du cadran avance de deux dents. Voilà pourquoi Devrine aurait doublé les dents du cylindre !! (C'est la première hypothèse)

Cadran de T1822 Double numérotation	-Vue arrière du cadran monté sur roue denté de 40 dents. -Détail des cylindres dont les dentures sont doublées.

 

Projection des cadrans sur le chariot totalisateur de T1822

 

C) 1848

Vers 1846,  Thomas trouve la perle rare, Piolaine,  un jeune ouvrier de talent qui est le fils d’un horloger de Neuilly. Il eut la charge de fabriquer une machine entièrement nouvelle. Ce ne fut pas chose facile, ..., mais finalement, en juillet 1848, la machine sort des ateliers !! Nombre d’entre vous connaissent cette beauté qui fut vendue chez Christie’s en 1996 pour un peu plus de 100 000 livres sterling ! Un rêve de collectionneur ….

T1848

Sur le plan mécanique, T1848 a des cylindres tout à fait particuliers. Ceux-ci possèdent en effet neuf dents, plus une, rétractile, qui vient se loger dans le corps du cylindre. En phase de retenue, elle sort de son logement et se positionne au même niveau que les neuf autres. Elle est plus longue que le cylindre lui-même, ce qui lui permet d'engrener avec la roue amovible A (celle que déplace le curseur) quelque soit sa position le long du cylindre (de 0 à 9). Ceci constitue une différence fondamentale avec tous les autres modèles d'arithmomètres qui possédaient une roue de retenue dédiée. Ici elle a été tout bonnement supprimée. En fin de rotation, une rampe hélicoïdale la repositionne en phase de non engrenage.

Cylindre T1849

D) 1850-1907

C'est à partir de 1850 que le cylindre prend sa forme définitive, soit 9 dents réparties sur 9/20 de la circonférence du cylindre. Les 11/20 restant servent à la gestion des retenues, notamment en cascade. Cette configuration a permis de construire des arithmomètres de 10, voir 11 chiffres à l'inscripteur.

T1850	T1852
T1863	T1865
Coupe d'un arithmomètre T1865
Cylindre T1865 (Dentures)	Cylindre T1865 (Zone vierge du cylindre)

E) Tableau récapitulatif